FFT

Die Fouriertransformation FT überführt eine Funktion $f(x)$ in ihre frequenzabhängige Darstellung $F(\omega)$.

Die Diskrete Fouriertransformation DFT ist eine Fouriertransformation, die diskrete endliche Werte von $\vec{v_e}:=f[\vec{x}]$ in die frequenzabhängigen Anteile $\vec{v_b}:=F[\vec{\omega}]$ überführt. Die IDFT invertiert die Transformation.

IDFT: $v_j = \sum_{k=0}^{n-1} c_k \omega^{jk}$, $\omega = e^{2 \pi i / m}$ ist Einheitswurzel: $\omega^n = 1$

DFT: $c_k = \frac{1}{n} \sum_{j=0}^{n-1} v_j \overline{\omega}^{jk}$

Äquivalenzen:

• Die DFT transformiert den Vektor $v_e$ in die Fourier-Basis $B$:
  $v_b = B^{-1}v_e, B^{-1} = \frac{1}{n} B^H$.
  Die IDFT transformiert den Vektor $F$ zurück in die kanonische (Einheits-) Basis:
  $v_e = B v_b$.

  Die Fourier-Basis lautet:

  $B^{-1} = \begin{pmatrix} 1 & 1 & 1 & ... \\ 1 & \omega & \omega^2 & ...\\ 1 & \omega^2 & \omega^4 & ...\\ ...& ... & ... & ... \end{pmatrix}$

• Die DFT/IDFT ist Interpolation $y_j = \sum_{k=0}^{n-1} c_k g_k(x_j)$ an den Stützstellen $g_k(x_j)=\omega^{jk}$

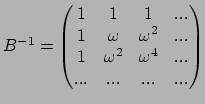
Analyse: Das Matrix-Vektor-Produkt hat Aufwand $O(n^2)$.

Algorithmus:
Die Fast Fourier Transformation FFT berechnet die DFT eines Vektors $\vec{v}$ aus zwei DFTs halber Länge der geraden und ungeraden Koeffizienten und Kombination der Ergebnisvektoren miteinander in $O(n \log n)$.

Definition:
Die (diskrete) Faltung (convolution) berechnet das Integral des Produkts zweier Funktionen, wobei eine Funktion achsengespiegelt wird.
$c_i = \sum_{k=-\inf}^{\inf} a_k b_{i-k}$
Die Faltung ist kommutativ und assoziativ, und hat Laufzeit $O(n^2)$. Sie entspricht in der Fourierbasis dem Produkt der Fourierkoeffizienten, lässt sich also über FFT, Multiplikation und IDFT in Zeit $O(n \log n)$ lösen.

Definition:
Bei der Polynommultiplikation gilt es das Problem $A \cdot B$ zu lösen, mit $A,B$ Polynome mit Koeffizienten $a_i, b_i$.
$C = (\sum_{j=0}^{n-1} a_j x^j) \cdot (\sum_{k=0}^{n-1} b_k x^k) = \sum_{i=0}^{2i-2} c_i x^i$ mit $c_i = \sum_{k=0}^{i} a_k b_{i-k}$
Die Berechnung der $c_i$ entspricht genau der Faltung von $A$ mit $B$.